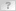i really doubt someone went in and made such a long fraction when they could just do .02.
It very common pratice to use bitshit instead of division.
its such acommon practive to avoid divison that compiler will try to avoid it when converitng you source code to machine code
The hardware in your cpu tries to avoid it even when its raw assmebly codes tries to do division.
Hence the old well known fdiv bug in the first generation Pentum becuase the lookup table in the CPU had some faulty entries in it
its not more difficult coding wise to do 32 bit shift vs 8 bits shifts from a human skill level
So I would have to disagree on all levels on this statements
The entire reason we do /256 or /1024 or /~4bll
is because these a hole numbers in binare and therefor can easily be replaced with bit shifts which is MUCH less stressfull in cpu ressource
To clarify its not coded as x/256 or x/1024 as in multiply with X and then divide with 256 or 1024
Is coded as multiple with X and move these bits 8bits over or 10bits over or in my case 32bits over ( when A bit get move outside the range of the the storage units it is "Deleted" hence why as default any divison is truncated / floored.
The code different is minimal
and its a very common practice among coders. compilers and hardware to do so
Besides the 32bit bit shift was just an example not necessarily a proof that we needed 32bits to achiever the precision to get the results from testing.
We might need way less. i just started in the extreme spectrum to show that its possible in binary math and the negate that the test was any kind of proof of decimal math
just because a computer reads it that way doesn’t mean it’s coded that way
The computer does EVERY calculations and the rounding in binary no matter how you type in code as a human.
P.S.
If im not mistaken ( and please correct me if you know)
but working with 32bit register in moderne cpu are faster than its 8 and 16bit counterparts. because of how the fetch and prediction units works in morderns cpu.
This was VERY apperanty in the Pentium PRO cpu as thier 16bits performance was horrible compared to its 32bit performance. but later on on the pentium2 som more shift on cpu isntruction to MicroOPS convertiob was improved ( E.G the cpu internally converted some 16bits math to 32bit math)
I would not be suprised if S.E. over the time changed the base divison going fomr 8bits hsift to 10bit shift to maybe 16 bit or 32bit shift.
all earlier data would still fit as before as you simply add more 0 to the X values. but never gear could archieved higher precision.
not saying there is any proof of it but its a possibility from both an accucacy and performance perspective